√ダウンロード (x y)^3 identity 478433-Complete the identity (x+y)^3

0(x−y,t)ϕ(0,y)∆0(x−y,t)ϕ t(0,y) dy (15) with ∆0(x−y,t)≡ 1 2 θ y−(x−t) −θ y−(xt) (161) ∇ 0(x−y,t)≡ 1 2 δ y−(x−t) δ y−(xt) (162) =∂ ∂t ∆ 0(x−y,t) Itisimportanttonoticethat,whilewehadprediction (ie,evolutionfrom prescribedinitial data)inmindwhenwedevised(15),theequationalsoworks retrodictively

Complete the identity (x+y)^3-Identités remarquables de degré 3 (a b) 3 = a 3 3a²b 3ab² b 3 (a b) 3 = a 3 3a²b 3ab² b 3 pour comprendre cette identité remarquable, on peut construire un cube de côté (a b) et exprimer de deux façons le volume du cubeAnswer (1 of 3) A classic way to prove inequalities is using AMGM inequality But my approach is different Here's my proof According to an algebraic identity, x^3 y^3 z^3 3xyz = (xyz)(x^2y^2z^2xyyzzx)(1) As x, y & z are positive numbers, (xyz) >

Complete the identity (x+y)^3のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Complete the identity (x+y)^3」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Complete the identity (x+y)^3」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Complete the identity (x+y)^3」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Complete the identity (x+y)^3」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Complete the identity (x+y)^3」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Complete the identity (x+y)^3」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「Complete the identity (x+y)^3」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

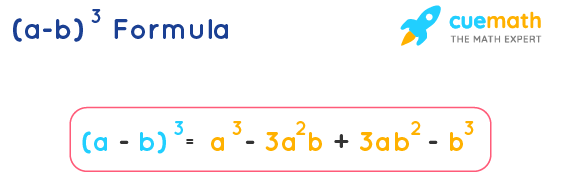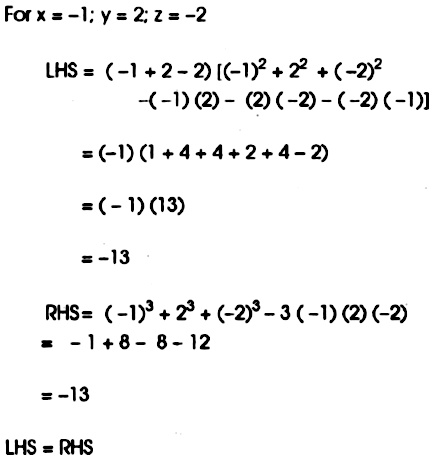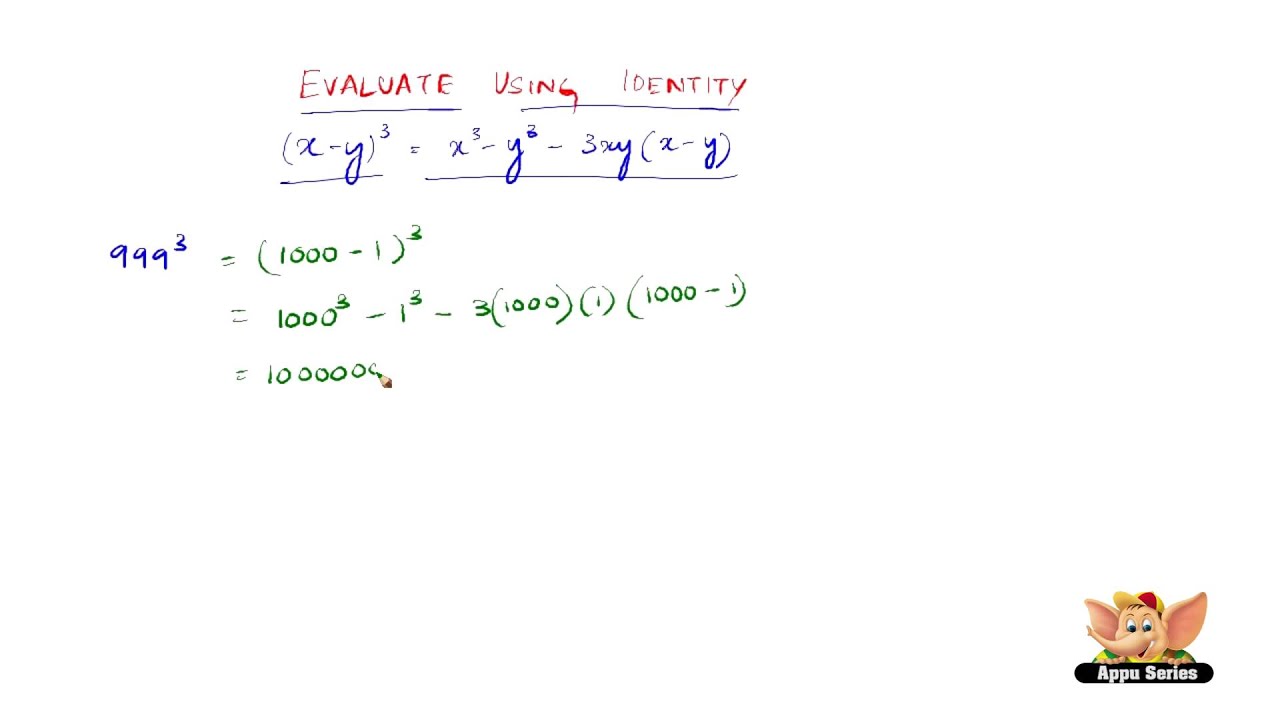「Complete the identity (x+y)^3」の画像ギャラリー、詳細は各画像をクリックしてください。

Solution By the algebraic identity, x 2 – y 2 = (x y) (x – y), we can write the given expression as;De Morgan's laws NAND x y = x y NOR x y = x y Redundancy laws The following laws will be proved with the basic laws Counterintuitively, it is sometimes necessary to complicate the formula before simplifying it

Incoming Term: (x+y)^3 identity, (x+y)^3 identity class 9, (x+y+z)^3 identity, complete the identity (x+y)^3,